Sub-problem 4d: Coordinated Operation With Left-Turn Protection

In order to estimate the proportion of skipped left-turn phases during the analysis time period, we need to estimate the probability that no left-turn vehicles will arrive during a cycle. For this purpose, it is common to assume that the left-turning vehicles will arrive at the intersection according to a Poisson distribution (a Poisson distribution reflects random arrivals). Assuming a Poisson distribution of arrivals, the probability of zero arrivals on any cycle may be computed as:

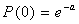
where a represents the average number of arrivals per cycle, based on the hourly volume.

Exhibit 1-41 shows the results of these computations. If the average length of a left-turn phase is less than 12 seconds, the difference is added to the phase time for the opposing through movement.

As an example, we will examine the average northbound phase times. The average cycle length at this intersection is 90-seconds, or 40 cycles per hour. The northbound left-turn volume is thirty-one vehicles per hour, which produces an average of 0.78 vehicles per cycle (31 vehicles per hour/40 cycles per hour). From the above equation we estimate zero arrivals on 46-percent of the cycles (e^-0.78), giving us an average phase time of 6.5 seconds (12 sec * (1-0.46)). Because this is less than the assumed maximum of 12-seconds green, we may add the difference in time (5.5 seconds) to the conflicting southbound through phase, producing 63.5 seconds of green (58 sec+5.5 sec).

The delay computations may use the average phase times for the through and left-turn movements determined from the table shown above.